Identifying and attacking the saddle point problem in high-dimensional non-convex optimization 리뷰

링크: https://arxiv.org/pdf/1406.2572.pdf

Intro

저차원에서의 기하학에 대한 경험을 고차원으로 적용할수 없다. 왜나하면 error function들은 차원이 커질수록 안장점의 개수는 지수적으로 증가하기 때문이다. 그리고 통계학, 랜덤 행렬이론, 신경망 이론, 선험적인 증거들로 비볼록함수를 최소화 하는것은 local minima의 문제가 아닌 안장점에서 비롯됨을 보인다. 특히, 고차원에서 안장점은 high error plateaus로 둘러 쌓여있어 학습을 극도로 낮추고 local minimum이 있다는 착각을 하게한다. 그래서 저자들은 기존의 SGD, quasi-Newton과는 다른 2차원 최적화 방법인 saddle-free newton method로 고차원에서 안장점을 탈출할 방법을 제시한다. 

 

The prevalence of saddle points in high dimensions

차원이 증가함에 따라 안장점은 지수적으로 증가함으로 고차원 비볼록 함수의 최적화를 방해하는 것은 local minima가 아닌 안장점이라는 주장을 검증하는 것에서 시작한다. 그에 대한 근거로 랜덤 가우시안 손실 함수에서 임계점의 성질을 살펴 본다.

α는 인덱스이고 e는 임계점에서 얻은 손실함수 값일때 e vs α 평면에서 임계점은 α가 0에서 1로 증가함에 따라 증가하는 단조 곡선에 분포하며,  e와 α의 관계를 시사한다(e ∝ α) . 

임계점이 O(1)일 확률은 고차원에서 매우 낮다. 이는 손실값 e를 가지는 임계점이 global minimum보다 훨씬 크다는것을 시사하며 안장점일 확률이 매우 높다. 이와 반대로 local minima(index = 0)는 global minimum과 같이 거의 같은 손실값 e를 가질 것이다. 이에 따라 직관적으로 임계점이 global minimum이거나 거의 같은 값을 가지지 않는 이상 손실함수 값이 더 내려가기 힘들다.

이를 random matrix theory를 이용해 설명하는데 차원이 큰 Gaussian random matrix의 고유값은 Wigner’s semicircular law를 따르고 이에 따라 고유값이 양수일 확률은 50%이다. 그리고 임계점에서의 헤세행렬의 고유값도 e에 따라 semicircular spectrum값이 이동된다는 것을 제외하면 위와 같다. global minimum에서 spectrum은 오른쪽으로 이동되기에 모든 고유값은 양수이다. e가 증가함에 따라 spectrum은 왼쪽으로 이동되며 고유값들은 음수가 된다. 이는 높은 손실함수 값을 가지는 안장점이 있음을 시사하고 이 점을 local minimum이라 착각할 수 있게 된다.

마지막으로 random matrix를 이용해 고차원의 손실함수를 살펴 보면, 차원이 커짐에 따라 고유값이 0일 확률은 낮아지고 양수/음수일 확률이 높아진다. 해세행렬의 고유값들이 양수/음수가 섞여있고 임계점이라면 그 점은 안장점이기때문에 대부분의 임계점은 안장점이 된다. 

Figure1. e  ∝ α and Eigenvalue per different errors

두개의 모델을 이용해 e와 α의 관계와 임계점에서 손실함수 값에 따른 고유값 분포를 보여주는 그래프이다. 위에 서술한 바와 같이 (a)와 (c)를 통해 e ∝ α를 볼 수 있고, 증가하는 단조함수에 분포됨을 볼 수 있다. (b), (d)를 통해 손실함수 값마다 고유값의 분포를 보이는데 손실함수 값이 클수록 위로 볼록인 방향축의 비율이 커진다. local minima는 위로 볼록하지 않기때문에 낮은 손실함수 값을 가진다.  

 

Experimental validation of the prevalence of saddle points

위 문단에서는 고차원에서 안장점이 많음을 이론적으로 밝혔고 이번 문단에서는 실험적으로 이를 밝힌다.

먼저 a single layer MLP에서 임계점이 e–α 평면에 어떻게 분포하는지, 헤세 고유값의 분포를 보기 위해 MNIST와 CIFAR로 학습한 MLP를 사용하였고 손실 함수에서 임계점을 알기 위해 Newton method를 사용하였다.

Figure2. Behaviors of different optimization methods near a saddle point,  (a):5x 2 − y 2 / (b): x 3 − 3xy2.  The yellow dot indicates the starting point.

앞서 이론적으로 봤듯이 임계점들은 증가하는 단조함수에 분포되어 있다. 고유값은 Wigner’s semicircular law를 따라 정확하게 분포하지는 않지만 손실값이 증가함에 따라 분포가 왼쪽으로 옮겨짐을 볼 수 있다. 따라서 높은 손실 값을 가지는 안장점이 많은 것은 학습에 문제를 일으킬 것임을 알 수 있다.

 

Dynamics of optimization algorithms near saddle points

안장점이 많을 때 다양한 최적화 알고리즘들이 안장점 근처에서 움직이는 방식에 대해 알아본다. 

먼저 gradient descent는 언제나 미분값이 안장점 근처로 맞게 방향을 가르킨다.

다음으로 Newton method는 최적화가 느려지는 문제를 미분값을 rescaling함으로써 해결한다. 이렇게 하면 미분값이 잘못된 방향을 가르킬 수 있다.

마지막으로 trust region는 비볼록 함수를 풀기 위한 실용적인 이차 미분 방법이다. 해세값을 damp하여 음의 곡률을 해결한다. 

 

Generalized trust region methods

안장점 문제를 해결하고 위의 세가지 방법을 개선하기 위하여 generalized trust region methods라는 새로운 방법을 도입한다. 이 방법은 trust region methods과 다르게 first-order Taylor expansion로 최소화를 시킨다. 그리고 norm의 constraint를 θ and θ+∆θ간의 거리로 대체한다. 이에 따라 generalized trust region methods식은 아래와 같다.

                                     ∆θ = arg min ∆θ Tk{f, θ, ∆θ} with k ∈ {1, 2}                            (1)

s. t. d(θ, θ + ∆θ) ≤ ∆. 

Attacking the saddle point problem

그러나 해세 행렬 H를 단순히 |H|로 대체할 수 없기에(증명 안됨) 거리를 범위를 이용하여 측정한다. 식 (1)에도 있는 ∆θ|H|∆θ이다. 이를 통해 새로운 식 ∆θ = −∇f|H| −1을 도출한다. 이 방법은 GD보다 낮은 곡률에서도 더(덜) 움직일 수 있고 안장점도 더 빠르게 탈출한다. Newton과 비교해도 이 방법은 안장점을 탈출할 수 있다.

Figure3. Empirical evaluation of different optimization algorithms for a single-layer MLP trained on the rescaled MNIST and CIFAR-10 dataset

저자들이 고안한 방법인 SFN이 최적화가 잘됨을 (b)와 (e)를 통해서 볼 수 있다. SGD와 Newton은 안장점 근처에 머무르는데 SFN은 빠르게 탈출한다. (c)와 (f)를 통해서 손실값이 커짐에 따라 고유값이 오른쪽으로 이동하는 것을 볼 수 있는데 SFN에서 이동을 더 많이 하므로 안장점을 잘 탈출할 것을 알 수 있다.

Experimental validation of the saddle-free Newton method

차원이 커짐에 따라 안장점의 개수가 지수적으로 증가한다는 저자들의 이론을 실험을 통해 증명한다. 그리고 최적화 함수들이 안장점에서 어떻게 되나를 보여준다.  

Figure4. Empirical results on training deep autoencoders on MNIST and recurrent neural network on Penn Treebank

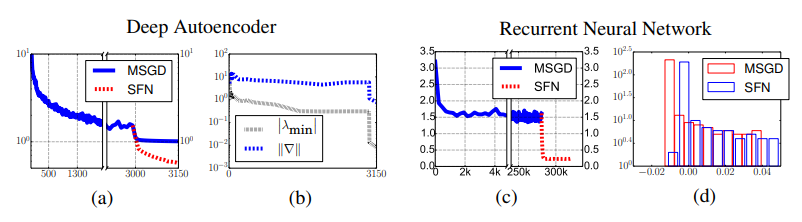
CNN과 RNN 모두에서 MSGD가 안장점 근처에 머무를 때 SFN은 빠르게 탈출하는 것을 볼 수 있다.

위의 실험은 CNN 층의 깊이가 7층인데도 탈출이 빠르게 이루어지고 헤세 고유값도 오른쪽으로 더 이동하므로 층이 깊은 모델에서도 SFN이 유효함을 밝힌다. 이는 RNN에서도 마찬가지이다. 

 

Summary

저자들은 고차원에서 높은 손실값을 가지는 local minima는 매우 드물고 임계점이 대부분은 안장점이라 주장한다. 이는 기존의 통념과는 다른 것이며 이 주장에 대한 근거로 이론적으로 e-α평면에서 임계점의 분포를 살펴보고 실험적으로 MLP모델에서 임계점들의 분포를 본다. 

그리고 안장점에서 탈출할 수 있는 새로운 최적화 방법을 제시하고, 이를 실험적으로 증명하여 기존의 최적화 함수들과 다르게 안장점에서 빠르게 탈출하여 손실함수 값이 낮아짐을 보인다. 

모델을 학습할 때 local mininum과 global minimum간의 차이가 없으므로 global minimum에 너무 집착할 필요가 없을 것 같다.