링크: https://arxiv.org/pdf/1706.03762.pdf
Introduction
게이트를 가진 RNN(LSTM)은 sequence modeling과 language modeling , 기계 번역에서 뛰어난 성과를 보였다. 그러나 RNN은 은닉상태 ht가 이전의 은닉상태 ht-1과 시각 t에서의 input의 함수이기에 sequential하고, 따라서 학습시 병렬화가 배제되어 긴 시계열을 다룰 때 좋지 않다.
attention은 input과 output간의 거리에 상관없이 dependencies modeling을 가능케 하여 다양한 분야에서 중요하게 사용되고 있다.
이 논문에선 recurrence를 없애고 encoder와 decoder 모두에 attention을 사용함으로써 input과 output간의 global dependencies를 이끌어 낼 수 있는 transformer라는 모델을 소개한다.
Background
Transformer는 self-attention에 기반하여 RNN이나 CNN없이 input으로부터 output을 연산한다. 기존의 모델들은 input과 output간의 거리가 멀어짐에 따라 요구되는 연산의 수는 선형적(ConvS2S) 혹은 지수적(ByteNet)으로 증가했었다. Transformer는 연산을 상수배로 줄이는데 성공했다.
Model Architecture
Encoder and Decoder Stacks
Transformer도 encoder와 decoder의 구조를 가지고 stacked self-attention와 point-wise한 fully connected layers를 가진다.

인코더는 N=6인 identical layers로 이루어져 있다. 각각의 층은 2개의 sub layer를 가지고 하나는 multi-head self-attention mechanism이며 나머지 하나는 positionwise fully connected feed-forward층이다. 두개의 sub layer에는 layer normalization를 하고 residual connection를 하였다 (residual connection는 잔여정보만 학습을 하면 되기에 학습이 빨라지고 수렴이 잘되는 효과가 있다(skip-connection?)). 이에 따라 각각의 sub layer의 출력은 LayerNorm(x + Sublayer(x))이고 차원 dmodel = 512이다.
디코더도 또한 N=6인 identical layers로 이루어져 있다. 인코더와는 다르게 각각의 층은 3개의 sub layer를 가지고 있다. 새로운 sub layer는 encoder의 출력을 입력으로 받아 multi-head attention연산을 한다. 디코더도 인코더처럼 sub layer에는 layer normalization이 되어있고 residual connection도 되어 있다.
Attention

논문에서 새로 도입한 두개의 어텐션 계층의 구조이다. Q는 query들을 합친 행렬, K는 차원 dk의 key값들을 합친 행렬 그리고 V는 차원 dv의 value들을 합친 행렬이다.
Scaled Dot-Product Attention은 이름에서도 알 수 있듯이 행렬들을 dot product 연산 후 softmax를 씌워 출력한다. 출력의 식은 다음과 같다.
$$ Attention(Q,K,V) = softmax(\frac{QK_{}^{T}}{\sqrt{d_{k}}})V $$
기존의 Dot-Product Attention과의 차이점은 dot product한 값을 √(dk)로 나누었다는 점인데 저자들은 dk가 커짐에 따라 dot product한 값(=QK)의 규모가 커져서 softmax함수가 미분값이 매우 작은 지역에 있게 되기에 이를 방지하기 위해서 √(dk)로 나누어준다.
Multi-Head Attention은 query, key, value들을 dk 평면에 서로 다른값으로 h번 사영시킨다. 그 값들을 합치고 다시 사영시키면 최종출력이 된다. 이는 Figure2의 오른쪽 그림에서 확인할 수 있다. 논문에선 h=8로 하였고 dmodel=512였으니 dv=dk=dmodel/h=64이다.
- Position-wise Feed-Forward Networks
인코더와 디코더 각각 완전연결 Feed-Forward 계층을 가지고 있다. 이 계층은 층마다 다른 가중치를 가지고 선형변환->RELU->선형변환 연산을 한다. 출력식은 다음과 같다.
$$ FFN(x) = max(0, xW1 + b1)W2 + b2 $$
- Embeddings and Softmax
input과 output을 dmodel차원의 벡터로 변환시키기 위해 Embedding계층을 사용한다. Embedding계층의 가중치에 √ dmodel을 곱한다. 다음에 나올 token(단어)의 확률들을 알기 위해 Softmax계층을 Decoder의 출력에 연결하고, 두개의 Embedding계층과 Softmax계층은 같은 가중치를 사용한다.
- Positional Encoding
트랜스포머는 recurrence layer와 convolution layer 둘 다 없기 때문에 입력의 절대적 혹은 상대적 위치에 대한 정보를 입력해주어야 한다. 이를 위해 Embedding 계층의 출력에 Positional Encoding의 출력을 더한다. Positional Encoding의 함수는 서로 다른 주기의 코사인, 사인 함수를 사용한다.
$$ PE_{(pos,2i)} = sin(\frac{pos}{10000^{\frac{2i}{d_{model}}}}) $$
$$ PE_{(pos,2i+1)} = cos(\frac{pos}{10000^{\frac{2i}{d_{model}}}}) $$
삼각함수를 사용함으로써 상대적 위치를 학습함에 따라 빠른 학습이 가능할것으로 추측된다.
Why Self-Attention
Self-Attention의 사용 이유에 대해 3가지 점을 고려한다.
첫번째로 각 층마다 연산 복잡도이다. 두번째는 병렬화 될 수 있는 연산의 양이다. 세번째는 네트워크 상의 long-range dependencies간의 거리이다. input과 output의 위치 간의 거리가 짧아질수록 long-range dependencies 연산이 빨라지기 때문이다.
첫번째와 두번째는 모델의 학습시간을 위해 고려하는 것 같고 세번째는 RNN의 문제점 중 하나인 long-range dependencies로 인한 모델의 성능저하 및 기울기소실 등 모델의 성능을 위해 고려하는 것 같다.

Table1에서 볼 수 있듯이 Self-Attention은 모든 위치를 연결하는데 상수시간이 필요하지만(O(1)) Recurrent는 O(n)이 걸림을 알 수 있다. 따라서 연산복잡도는 Self-Attention이 sequence의 길이n이 차원d보다 작을 때 Recurrent보다 빠르다. 또한 넓이 k가 n보다 작은 Single Convolutional layer는 넓이k때문에 Recurrent layer보다 연산량이 크고 연산량이 작은Separable convolutions이라 할지라도 Self-Attention과 연산량이 같고, 표현력은 Self-Attention이 더 좋기 때문에 Self-Attention 사용에 대한 당위성이 성립한다.
Training
Transformer를 학습시킬때 Optimizer로는 Adam(β1 = 0.9, β2 = 0.98 그리고 ε= 10^−9)를 사용하였고 학습률은 다음 공식을 사용하였다.
$$ lrate = d_{-0.5}^{model}*min(step num_{-0.5}, step num*warmup steps_{-1.5}) $$
warup steps는 4000이고 학습률은 √ (step num^-0.5)에 비례하여 감소한다.
정규화는 두가지 방법을 이용한다. 하나는 Residual Dropout, rate=0.1인,을 각각의 sub layer의 출력층, positional encodings 뒤 그리고 Embedding 층 뒤에 적용하였다.
나머지 하나는 Label Smoothing,ε= 10^−9,으로 perplexity는 감소하지만 정확도와 BLEU 점수는 올라간다.
Results
기존의 SOTA(State-of-the-art)들보다 BLEU점수와 연산속도 모두 더 뛰어난 것을 볼 수 있었다.
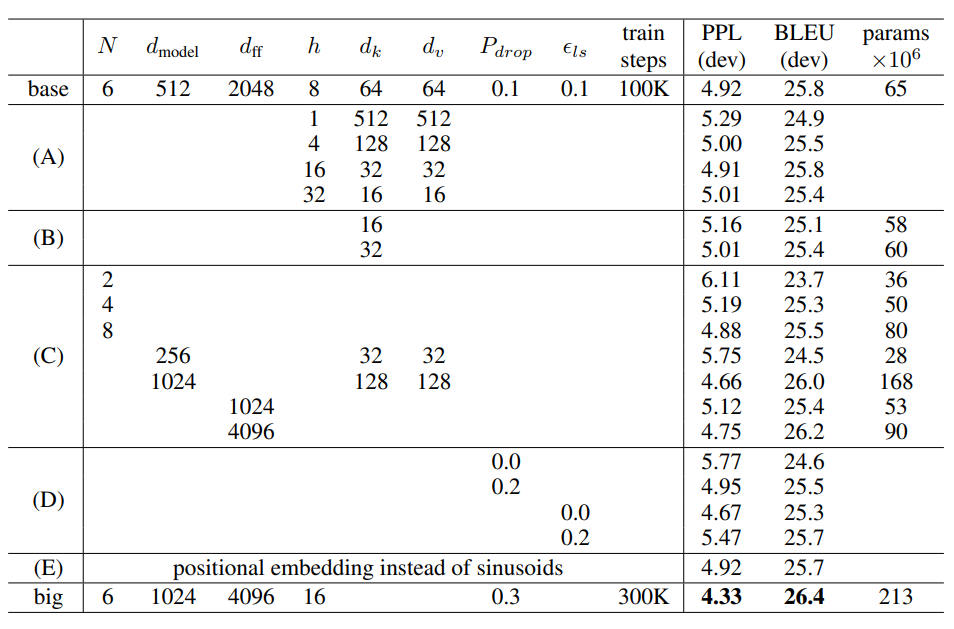
그 후 모델의 Hyper parameter들을 바꿔가며 성능을 측정했다. B행을 통해 attention key size인 dk가 감소하면 성능이 감소하는 것을 볼 수 있고 C,D행을 통해 모델이 커질수록 성능이 좋아지고, dropout이 오버피팅을 잘 막아줌을 보았다.
마지막으로 finetunning을 크게 진행하지 않더라도 전이학습을 통한 일반화 성능이 뛰어난 것을 보였다.
Summary
기존의 LSTM으로 만든 seq2seq와 다르게 Encoder와 Decoder 모두 Attention으로 이루어져 있다. 또한 Encoder와 Decoder가 각각 N개씩 있다.(논문에서 N=6)
Attention으로는 시계열 데이터의 위치정보를 기억할 수 없기에 Positional Encoding계층의 출력을 임베딩 계층의 출력에 더하여 위치정보를 기억한다. Positional Encoding계층은 삼각함수를 사용함으로써 상대적 위치를 기록한다.
Attention계층은 Dot-product한 값을 √(dk)로 나누어 Softmax함수값이 소실되지 않게 하는 Scaled Dot-product Attention계층을 쌓아 만든 Multi-head Attention계층을 사용하였다. Scaled Dot-product Attention계층은 내적을 통해 맥락벡터를 구하고 멀리 있는 값들과 유사성을 구하지 않기 위해 마스킹을 한다.
Attention계층뿐만 아니라 모든 sub layer에 residual connection을 하여 학습속도를 향상시키고 minima로 수렴이 잘 되게 하였다.
Transformer의 Hyper parameter들은 다음과 같다.
· dmodel: 인코더와 디코더에서의 정해진 입력과 출력의 크기
· dff: 은닉층의 크기
· num_heads: Figure2의 h로서 병렬연결된 갯수이다.
· num_layers: 트랜스포머에서 인코더와 디코더는 N개 존재한다. Figure1에서 N=numlayers으로 인코더와 디코더의 층수 이다.
'AI' 카테고리의 다른 글
| 모델 학습 시 데이터를 shuffle해야 하는 이유(배치 학습) (0) | 2022.10.04 |
|---|---|
| 캐글 타이타닉 생존자 예측 실습(Logistic Regression) (0) | 2022.09.28 |
| Deep Learning without Poor Local Minima 리뷰 (2) | 2022.09.21 |
| Identifying and attacking the saddle point problem in high-dimensional non-convex optimization 리뷰 (0) | 2022.09.20 |
| 손실함수의 그래프(Training Curve, Loss Landscape)와 최적화 방법 (0) | 2022.09.20 |
