여태 이론적으로 배운 내용들을 실제로 구현해보고, 머신러닝 라이브러리를 직접 사용해봄으로써 이론적으로 배운 내용을 복습할겸 캐글의 가장 간단한 Competition인 타이타닉 생존자 예측을 해보았다.
먼저 문제를 보았을 때 승객의 데이터를 이용하여 생존 유무를 예측하는 문제이므로 이진 분류문제라 생각하였다(죽음=0, 생존=1).
이진 분류를 위한 알고리즘에는 Logistic Regression, KNN, SVM, Ensemble(XGB, Bagging Decision Tree, Random Forest..), Decision Tree, LGBM등 다양한 기법들이 있지만 그 중 Logisitic Regression, XGB를 이용하여 문제를 풀어보기로 했다.
우선 SVM은 데이터의 차원이 11차원으로 크지 않아 pass했고 LGBM은 데이터의 크기가 너무 작아 과적합의 우려로 패스했다. LGBM 공식문서에서도 데이터가 만건 이상인 문제에 대해 쓸 것을 권장하고 있다.
문제의 데이터셋이 작아 기본적인 LR로도 데이터 전처리를 잘한다면 좋은 결과를 얻을 수 있을것이라 생각했고, XGB는 결측치가 있어도 돌릴 수 있어 결측치를 처리 했을 때와 안 했을때의 차이를 보고싶어 써봤지만 데이터의 크기가 작은 고편향/저분산 문제이기에 Boosting기법으로 좋은 결과를 얻을 수 있을까는 조금 회의적이였다. XGB로 푼건 추후 포스팅하겠다.
물론 머신러닝에 절대적인건 없어 모든 알고리즘 기법을 사용해본 후 비교해보는게 제일 이상적이겠지만 시간관계상 알고리즘들을 취사선택하여 문제를 풀어보았다.
코딩환경은 구글 코랩을 사용하였다.
!mkdir ~/.kaggle
!touch ~/.kaggle/kaggle.json
api_token = {"username":"username","key":"key"}
import json
with open('/root/.kaggle/kaggle.json', 'w') as file:
json.dump(api_token, file)
!chmod 600 ~/.kaggle/kaggle.json
!kaggle competitions download -c titanic
%cd /content/
!unzip -qq "/content/titanic.zip"먼저 data를 가져오기 위해 kaggle api를 사용하였고 코랩은 리눅스 기반이므로 리눅스 명령어를 통하여 다운로드한 폴더에 접근하여 압축파일을 풀어주었다.
import pandas as pd
import seaborn as sns
import numpy as np
train = pd.read_csv('/content/train.csv')
train.head()
test = pd.read_csv('/content/test.csv')
test.head()
sns.set(rc = {'figure.figsize':(10,6)})
sns.heatmap(train.corr(), annot = True, fmt='.2g',cmap= 'YlGnBu')

그 후 pandas를 이용해서 데이터 파일을 읽고 csv의 head를 불러 데이터 파일이 어떤형태인지 보았다.
데이터들을 우선 11열로 구성되어 있고 Numercial data, Categorical data 모두 있음을 볼 수 있다. 상관계수를 보기 위해 heatmap을 보았는데 상관계수가 낮은 독립변수들은 제외하기 위해서이다.
PassengerId는 상관계수도 너무 낮고 직관적으로 생존과 연관이 없을 것 같아 독립변수에서 제외하는데 이상이 없었다. 그런데 SibSp와 Parch는 배에 탄 사촌/직계가족의 수로 생존과 상관관계가 있을줄 알았는데 상관계수가 [0.1~0.1] 사이에 있어 생존과 상관관계가 낮음을 알 수 있었다. 내 직관과 상관계수가 서로 달라 SIbSp와 Parch는 제외했을 때 안했을 때의 예측정확도를 각각 비교해보아야 겠다.
Age의 상관계수도 낮았는데 이 역시 직관과는 좀 벗어나 있었다. 왜냐하면 노약자가 배려를 많이 받기때문에 생존률이 높을것이라고 생각했기 때문이다. 나이대 별 히스토그램을 봄으로써 약간의 도움을 받을 수 있었다.
plt.hist(train['Age'], cumulative=True, label='cumulative=True')
plt.hist(train['Age'], cumulative=False, label='cumulative=False')
plt.legend()
plt.show()
히스토그램을 통해 볼 수 있듯이 노약자라고 할만한 0~10세와 60~70세는 전체에서 차지하는 비율이 얼마 되지 않는다. 전체를 합쳐도 10%대라서 나이가 생존과 상관관계가 낮게 나온게 아닐까 추측을 해본다.
print("Train data missed values:\n")
print(train.isnull().sum())
print("-----------------------------------")
print("Test data missed values:\n")
print(test.isnull().sum())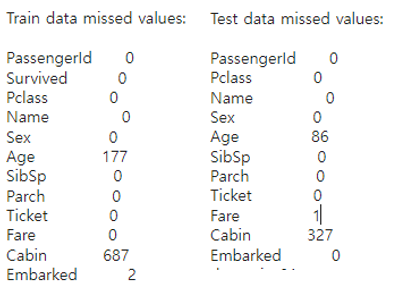
그 후 독립변수 선택, 전처리에 도움을 더 받기 위해 결측치들을 확인하였다. train, test 데이터 모두 Age와 Cabin의 결측치가 큼을 알 수 있다. 결측치를 채우는데 도움을 받기 위해 data들의 분포를 확인하였다.
train.describe()
train.describe(include=['O'])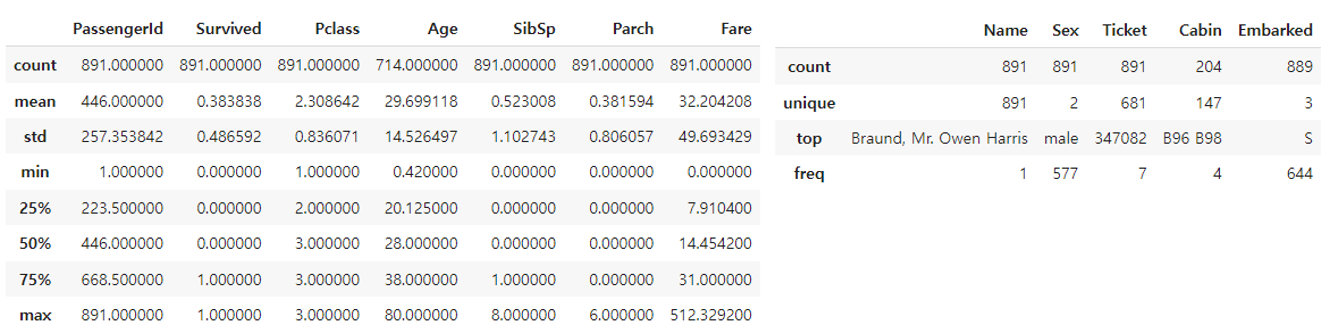
먼저 Numercial Data(Figure5의 왼쪽표)들의 분포를 먼저 보면 Age와 Fare는 다른 값들에 비해 범위가 넓음을 볼 수 있었고 이에 따라 정규화를 진행해야겠다는 추론을 하였다. 오른쪽의 Categorical Data를 보면 겹치는 이름이 없다는 점이 눈에 띄었다. 그리고 Ticket과 Cabin은 중복이 23~8%정도 있음을 알 수 있었다. Cabin은 결측치가 너무 크고 중복도 많아 결측치를 채우는데 어려움이 있을 것 같아 제외해야겠다고 생각하였다.
Name은 고민이 되는 변수였으나 삭제하는 것이 나을 것 같다고 생각했다. 이름을 통해서 얻을 수 있는 정보는 성과 호칭이다. 성을 통해 가족관계를 알 수 있으나 성이 겹칠 수 있어 적절치 않다고 생각했다. 호칭은 Mr, Mrs, Miss 등이 있는데 이는 성별과 나이가 합쳐진 변수라고 생각해서 다른 독립변수들로 표현 가능하다 생각했다. 따라서 Name 변수는 삭제하였다.
마지막으로 Categorical Data들의 생존과 상관관계를 알기 위해 EDA를 사용하였다.
import matplotlib.pyplot as plt
def survived_bar_plot(feature):
plt.figure(figsize = (6,4))
sns.barplot(data = train , x = feature , y = "Survived").set_title(f"{feature} Vs Survived")
plt.show()
survived_bar_plot('Sex')
survived_bar_plot('Embarked')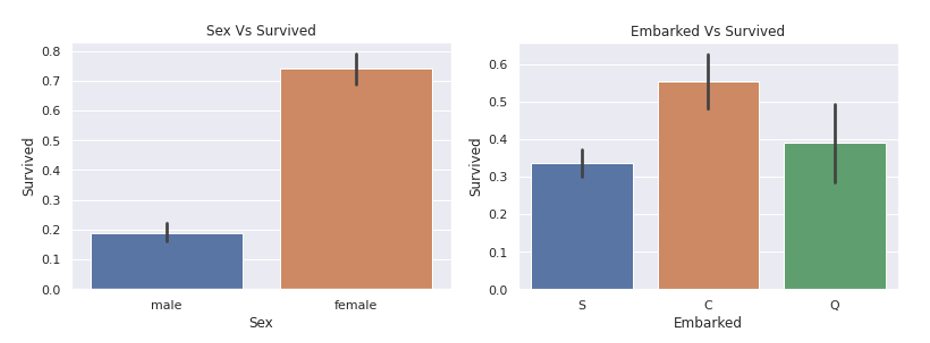
시각화를 통해 sex, embarked 각각의 생존확률과 상관관계를 보았는데 상관관계가 있어보인다. 성별에서는 극명히 보이고 탑승한 항구에서도 생존률에 차이를 보이는 등 상관관계가 있어 보였다. heatmap에서 객실등급(Pclass)과 요금(Fare)이 생존률과 가장 큰 상관관계를 가지는 것을 볼 수 있었는데 탑승한 항구가 부유한 동네에 있나 가난한 동네에 있나에 따라 달라지는 것 같다.
Ticket에 따른 생존률도 확인하였는데 중복이 적어 같은 티켓을 가진 승객이 3~4명뿐이라 생존률에 유의미한 관계를 가진다고 보기 어려워 보였다.
import numpy as np
import pandas as pd
from sklearn.impute import KNNImputer
imputer = KNNImputer(n_neighbors=5)
# 필요 없는 col 지우기
train.drop(columns = ["PassengerId", "Ticket", "Cabin", "Name"] , inplace = True)
test_pd = test["PassengerId"] # 모델 추론을 위해 미리 뽑아놓음
test.drop(columns = ["PassengerId", "Ticket", "Cabin", "Name"] , inplace = True)
# Embarked변수 numercial data로
for index, embark in enumerate(['C', 'Q', 'S']):
train.loc[(train['Embarked'] == embark), 'Embarked'] = index
test.loc[(test['Embarked'] == embark), 'Embarked'] = index
# Sex변수 numercial data로
for index_, sex in enumerate(['male', 'female']):
train.loc[(train['Sex'] == sex), 'Sex'] = index_
test.loc[(test['Sex'] == sex), 'Sex'] = index_
# KNN을 이용한 결측치 채우기
train = pd.DataFrame(imputer.fit_transform(train), columns = train.columns)
test = pd.DataFrame(imputer.fit_transform(test), columns = test.columns)
#최대최소 정규화
train['Age'] = (train['Age'] - train['Age'].min())/(train['Age'].max()-train['Age'].min())
train['Fare'] = (train['Fare'] - train['Fare'].min())/(train['Fare'].max()-train['Fare'].min())
test['Age'] = (test['Age'] - test['Age'].min())/(test['Age'].max()-test['Age'].min())
test['Fare'] = (test['Fare'] - test['Fare'].min())/(test['Fare'].max()-test['Fare'].min())
train.head()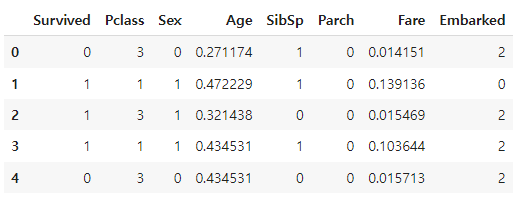
데이터 분석에 따라서 데이터에 전처리를 해주었다. 상관계수가 낮거나 사용하기 어려운값들은 버리고, 범위가 다른 독립변수들에 비해 큰 변수는 정규화를 해주고 결측치들을 채워주었다. 그리고 Categorical Data를 Numerical Data로 변환해주었다. 결측치는 독립변수들끼리 상관관계가 있기 때문에 KNN imputation을 이용하였다. Age와 Pclass와의 상관계수는 0.34로 꽤 높기에 결측치를 채우는 데에 선형회귀를 사용하는 것도 방법일 것같다.
데이터 전처리를 모두하였으니 모델을 만들어 입력을 넣어보았다.
import torch
from torch import nn
y_train , x_train = train["Survived"].astype('float64'), train.drop(labels = ["Survived"],axis = 1)
x_train = torch.tensor(x_train.values.astype(np.float32))
y_train = torch.tensor(y_train.values.astype(np.float32)).reshape(891, 1)
print(f"X_train shape is = {x_train.shape}" )
print(f"Y_train shape is = {y_train.shape}" )
model = nn.Sequential(nn.Linear(in_features=7, out_features=1, bias=True), nn.Sigmoid())
loss_function = nn.BCELoss()
optimizer = torch.optim.Adam(params=model.parameters(), lr=0.01)
epochs = 3000이진 로지스틱 회귀이기에 출력층에 시그모이드 함수를 쓰고 손실함수로는 이진분류이므로 Binary Cross Entropy를 사용하였다. 에폭은 3000으로 임의로 두었다.
for epoch in range(epochs):
prediction_ = model(x_train)
loss = loss_function(input=prediction_, target=y_train)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 10 == 0:
prediction = prediction_ >= torch.FloatTensor([0.5])
correct_prediction = prediction.float() == y_train
accuracy = correct_prediction.sum().item() / len(correct_prediction)
print(f'Epoch: {epoch}, Accuracy: {accuracy*100:.2f}%, Current Loss: {loss:.4f}')정확도는 81%, 손실함수값은 0.43에 수렴하였다. 제출한 점수는 0.76이였다.
앞으로 모델을 더 개선해 보겠다. 먼저 배치크기를 줄여 보았다. 왜냐하면 배치 크기와 학습률은 일반적으로 양의 상관관계를 가지고 있는데 배치 크기가 너무 커서 학습률을 더 줄여도 학습효과가 나아지지 않기 때문이다.
import torch
from torch import nn
from torch.utils.data import Dataset, DataLoader, random_split, TensorDataset
y_train , x_train = train["Survived"].astype('float64'), train.drop(labels = ["Survived"],axis = 1)
x_train = torch.tensor(x_train.values.astype(np.float32))
y_train = torch.tensor(y_train.values.astype(np.float32)).reshape(891, 1)
dataset = TensorDataset(x_train, y_train)
test_size = int(len(dataset)*0.2)
train_size = len(dataset)- int(len(dataset)*0.2)
train_dataset, test_dataset = random_split(dataset, [train_size, test_size])
print(f"Training Data Size : {len(train_dataset)}")
print(f"Testing Data Size : {len(test_dataset)}")
train_dataloader = DataLoader(train_dataset, batch_size=16, shuffle=True, drop_last=True)
test_dataloader = DataLoader(test_dataset, batch_size=4, shuffle=True, drop_last=True)데이터를 불러오는 코드에 배치를 추가하였고 오버피팅이 일어나는 지를 보기 위해 train data를 8:2로 나누어 test data를 추가하였다.
분포를 위해 radom하게 split하였고 모델이 데이터의 순서에 익숙해지는 것을 방지하기 위해서 shuffle또한 해주었다. batch size는 trian data는 일반적으로 쓰이는 16을 사용하였고 train data와 test data의 크기비율이 4:1이기 때문에 test data의 batch size는 4로 하였다. 배치 사이즈를 기존의 891에서 16으로 줄임으로써 학습률도 1e^-3으로 줄였다.
loss_min = np.Inf
for epoch in range(epochs):
print(f"Epoch {epoch+1}\n-------------------------------")
for batch, (x_batch, y_batch) in enumerate(train_dataloader):
prediction_ = model(x_batch)
loss = loss_function(input=prediction_, target=y_batch)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if batch % 10 == 0:
prediction = prediction_ >= torch.FloatTensor([0.5])
correct_prediction = prediction.float() == y_batch
accuracy = correct_prediction.sum().item() / len(correct_prediction)
current, size = len(x_batch)*batch, (len(train_dataloader.dataset))
print(f"Loss: {loss:>4f}, Accuracy: {accuracy*100:.2f}% | [{current:>5d}/{size:>5d}]")
if loss <= loss_min:
print('==== Loss decreased ({:6f} ===> {:6f}). Saving the model! ===='.format(loss_min, loss))
torch.save(model.state_dict(), 'model.pth')
loss_min = loss
size = len(test_dataloader.dataset)
num_batches = len(test_dataloader)
model.eval()
test_loss, correct = 0, 0
with torch.no_grad():
for X, y in test_dataloader:
pred = model(X)
test_loss += loss_function(pred, y)
pred = pred >= torch.FloatTensor([0.5])
correct += (pred.float() == y).type(torch.float).sum().item()
test_loss /= num_batches
correct /= size
print(f"Test Error: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {test_loss:>8f} \n")
print(loss_min)기존의 코드에서 세가지를 추가하였다.
첫번째로 미니배치 학습을 위해서 파이썬의 enumerate함수를 이용해 index와 value를 모델에 넣어주었다. 학습률과 배치크기가 작아졌기에 loss값이 더 줄어들 것을 기대하였다.
두번째로 오버피팅이 일어나는 지를 보기 위해서 test data를 이용해 각 epoch마다 model을 평가하였다.
세번째로 Loss값이 작아졌을 때 모델의 상태를 저장하여 가장 좋은 상태로 평가할 수 있게 하였다.
학습을 한 결과 test error는 0.41로 수렴하고 정확도는 마찬가지로 81%에 수렴하였다. train data의 정확도는 변동폭이 크고 손실함수역시 그러하였다.
추가로 Optimizer를 Adam, SGD 두개를 비교하였다.
배치크기를 줄이는 것으로 정확도에 큰 향상을 보이진 못했다. loss값은 소폭 줄어 캐글 제출점수는 0.768로 아주 조금 올랐다. 하지만 Optimizer를 SGD로 바꿧을때 정확도는 82%정도로 조금 더 올랐고 loss도 소폭 더 떨어져 캐글 제출점수는 0.775로 소폭 더 상승했다.
마지막으로 표현력을 더하고(비선형성 추가) 오버피팅을 방지하기 위해 은닉층과 활성화함수, 드랍아웃 기법을 더해보았다.
class NeuralNetwork(nn.Module):
def __init__(self):
super(NeuralNetwork, self).__init__()
self.flatten = nn.Flatten()
self.linear_relu_stack = nn.Sequential(
nn.Linear(7, 50),
nn.Dropout(0.25),
nn.ReLU(),
nn.Linear(50,10),
nn.ReLU(),
nn.Linear(10,1),
nn.Sigmoid()
)
def forward(self, x):
logits = self.linear_relu_stack(x)
return logits데이터셋의 크기가 작기때문에 Dropout rate는 작게 설정하였다. 은닉층을 두개 더하고 ReLU를 활성화 함수로 씀으로써 비선형성을 더 잘 표현하여 예측력이 높아질 것이라 기대하였다.
정확도는 그대로였으나 loss가 0.38로 떨어져 캐글점수는 0.7822로 2400등으로 마무리하였다. 다른 사람들의 코드를 보니 데이터의 전처리쪽에서 더 신경을 쓴다면 더 좋은 예측력을 가진 모델을 만들 수 있을 것 같다.
'AI' 카테고리의 다른 글
| LightGBM: A Highly Efficient Gradient BoostingDecision Tree (0) | 2022.10.11 |
|---|---|
| 모델 학습 시 데이터를 shuffle해야 하는 이유(배치 학습) (0) | 2022.10.04 |
| Attention Is All You Need 리뷰 (0) | 2022.09.22 |
| Deep Learning without Poor Local Minima 리뷰 (2) | 2022.09.21 |
| Identifying and attacking the saddle point problem in high-dimensional non-convex optimization 리뷰 (0) | 2022.09.20 |
