Visualizing the Loss Landscape of Neural Nets 리뷰

논문: https://arxiv.org/pdf/1712.09913v3.pdf

Intro

손실함수를 시각화하는 방법에 대해 궁금해하던 중 발견한 논문이다. 왜냐하면 손실함수를 시각화하여 봄으로써 최적화함수의 선택에 도움이 될 것이라고 생각했기 때문이다.

이 논문에서는 단순 손실함수 시각화뿐 아니라 모델의 구조, 최적화 함수, Weight Decay와 skip-connection 그리고 배치 사이즈에 따른 손실함수의 변화를 시각화하여 보여줌으로써 모델에 주는 영향을 직관적으로 알 수 있게 한다. 

 

The Basics of Loss Function Visualization

이 논문에선 손실함수를 표현하는 방법으로 '1-Dimensional Linear Interpolation'와 'Filter-Wise Normalization'를 소개한다. 

'1-Dimensional Linear Interpolation'는 초기 파라미터 θ와 학습된 파라미터 θ' 사이를 이어 손실함수의 값을 표현하고자 한다. 변수 θ를 일직선상에 표현하기 위한 방법으로 θ(α) = (1−α)θ+αθ'라는 식을 사용했다. 이 방법은 비볼록함수를 표현하기 힘들고 배치정규화와 invariance symmetries는 고려하지 않아 minima에서 flatness나 sharpness를 비교할 때 잘못 될 수 있다 한다.

그다음으로 'Filter-Wise Normalization'라는 방법을 소개하기 위해 'Contour Plots & Random Directions'를 소개한다. Contour Plots는 3차원 상의 면을 Contour(같은 값을 가지는 점들을 연결한 곡선, 등치선)로 2차원상에 표현하는 방법이다. 그리고 랜덤하게 방향벡터 δ와 η를 골라 좌표를 식 f(α, β) = L(θ ∗ + αδ + βη) (1)을 통해 2차원 상에 시각화 한다.그러나

아직 몇가지 문제가 남아 있었다. 식 (1)을 통해서는 손실함수의 본질적인 기하학적 성질을 표현할 수 없기에 서로 다른 모델 혹은 최적화함수를 비교할 수 없었다. 왜냐하면 가중치의 scale invariance때문이다. 

 

이를 해결하기 위해 식 (1)을 통해 이제 'Filter-Wise Normalization'라는 시각화 방법을 사용한다. 파라미터 θ를 가진 모델의 방향베겉를 구하기 위해 θ와 호환되는 랜덤 가우시안 벡터 d를 이용한다. 그리고 벡터 d를 θ와 같은 norm을 가지게 하기 위해 아래 식을 이용해 정규화한다. 

$$ d_{i,j}\leftarrow \frac{d_{i,j}}{\left\|d_{i,j} \right\|}\left\|\Theta_{i,j} \right\|   $$ 

 

이 방법을 통해 시각화한 자료와 기존의 '1-Dimensional Linear Interpolation'을 이용해 시각화한 자료를 각각 비교하였다.

Figure1. 1D linear interpolation of VGG-9 solutions, (a): small batch / (d): large-batch, solid line: train / dashed line: test

먼저 기존의 '1-Dimensional Linear Interpolation'을 이용해 시각화한 그래프이다. 

기존의 방법은 Weight Decay를 키고 켬에 따라 그래프의 sharpness함이 뒤바뀜을 (a)와 (d)를 통해 볼 수 있다. 또한 (c), (f)를 통해 배치 사이즈는 그대로임에도 sharpness함이 달라짐을 볼 수있다. 마지막으로 (b), (e)에서 에폭수가 증가함에 따라 배치사이즈가 작을 때는 ||θ2||가 커지지만, 배치 사이즈가 큰 경우는 거의 변화가 없음을 볼 수 있다. 그러나 Weight Decay를 적용하면 반대로 배치사이즈가 작은 경우가 변화가 더 커지고 Weight Decay가 없을때는 배치사이즈가 작을 때 Flat Minima에 도달하고 Weight Decay가 있을 때는 배치사이즈가 클 때가 Sharp Minima에 도달함을 볼 수 있다.

 

Proposed Visualization: Filter-Wise Normalization

Figure2. The 1D and 2D visualization of solutions obtained using SGD with different weight decay and batch size, weight decay/ batch size / test error

다음으로 'Filter-Wise Normalization'를 이용해 시각화한 자료이다. 

이 자료들로 기존의 시각화는 일관성이 없음을 알 수 있고 이는 저자들이 밝힌 Scale Invariance의 영향때문이다.

반면에 저자들이 소개한 새로운 방법은 일관된 경향성을 가짐을 알 수 있다. (e)와 (f)를 통해 배치 사이즈가 커지면 contour가 작아지고 더 sharp해짐을 볼 수 있다. 이는 weight decay를 적용했을 때도 마찬가지임을 (g)와 (h)를 통해 볼 수 있었다.

 

이 방법을 통해 일관되게 변화를 가지는 걸 볼 수 있었지만, 고차원의 손실함수 표면의 차원을 엄청나게 줄였기 때문에 저자들은 convexity를 맞게 시각화 중인지 보기 위해, 볼록함의 정도를 보기 위해 해세 고유값인 principle curvatures을 계산한다. 왜냐하면 볼록함수는 음이 아닌 곡률 값을 가지고 비볼록 함수는 음의 곡률 값을 가지기 때문이다. 따라서 차원이 감소된 plot에서 비볼록함이 존재한다면, 비볼록함은 원래 차원의 평면에서도 있어야 한다. 그러나 차원이 감소된 표면에서 볼록함이 있다 하더라도 원래 차원이 볼록한 것은 아니고 원래 차원에서 볼록함이 우세하다는 것을 의미한다.

 

여기에 저자들은 시각화(저차원으로의)를 통해 포착하지 못한 비볼록함이 있을까 판단할 수 있는 eigenvalues of the Hessian인 λmin and λmax를 계산한다. 그 후 |λmin/λmax|를 손실함수 표면 전체에 계산해 평면상에 나타낸다.

 

Figure3. Blue color: convex region / yellow: negative curvature

해세 고유값들의 비율을 나타낸 맵이 저자들이 소개한 방법인 'Filter-Wise Normalization'로 시각화한 맵과 볼록한곳, 오목한곳이 일치함을 볼 수 있다. 

 

이제 'Filter-Wise Normalization'로 시각화한 맵의 신뢰성에 대한 근거를 두개나 보았으니, 다른 모델들과 파라미터들도 'Filter-Wise Normalization'를 통해 시각화하여 파라미터의 변화에 따른 모델의 변화를 살펴본다.

 

먼저 네트워크의 깊이와 skip connection의 유무에 따른 모델의 차이에 대해 살펴본다.

Figure4. 2D visualization of the loss surface of ResNet and ResNet-noshort with different depth

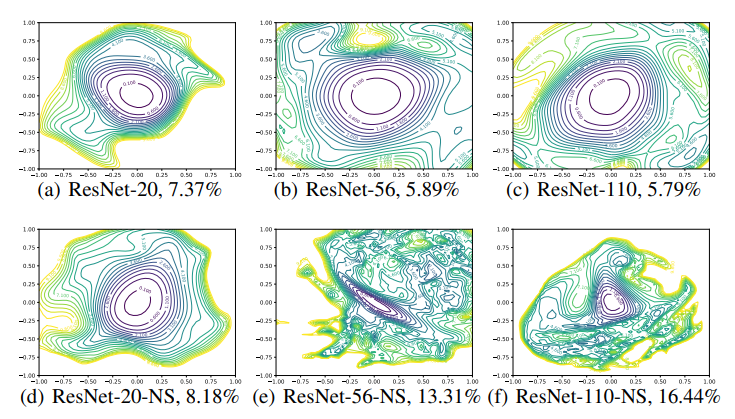
먼저 skip-connection이 없는 (d), (e), (f)부터 보면 (d)는 비볼록점이 거의 없는, 중앙에 볼록한 등치선이 지배적인 것을 볼 수 있고 이에 따라 학습에 효율적임을 알 수 있다. 그러나 깊이가 깊어지면 비볼록점이 점점 우세해지는 것을 볼 수 있다(노란색 선). 볼록함에서 chaotic함으로 변해가고, 몇몇 미분값들은 global minimum인 center를 가르키지 않는다. 또한 특정 값들간의 거리가 매우 커지며 가파라진다. 깊이가 깊어짐에 따라 학습이 어려워지는 이유를 알 수 있다.skip-connection이 있는 (a), (b), (c)를 보면 skip-connection의 효과가 아주 큼을 알 수 있다. 층이 얇은{(a), (d)} 모델에서는 그 효과가 두드러지지 않지만 층이 깊어질수록 기울기 폭발, 비볼록함을 방지함을 알 수 있고 (a), (b), 그리고 (c) 그래프는 거의 차이가 없음을 볼 수 있다.

 

그 다음으로는 층마다 컨볼루션 필터 숫자에 따른 변화를 보기 위해(얇은 모델과 넓은 모델) narrow CIFAR-optimized ResNets (ResNet-56)와 Wide-ResNets를 시각화하고 비교를 한다.

Figure5. Top: with self-connection / Botton: without self-connection, k: number of filters per layer

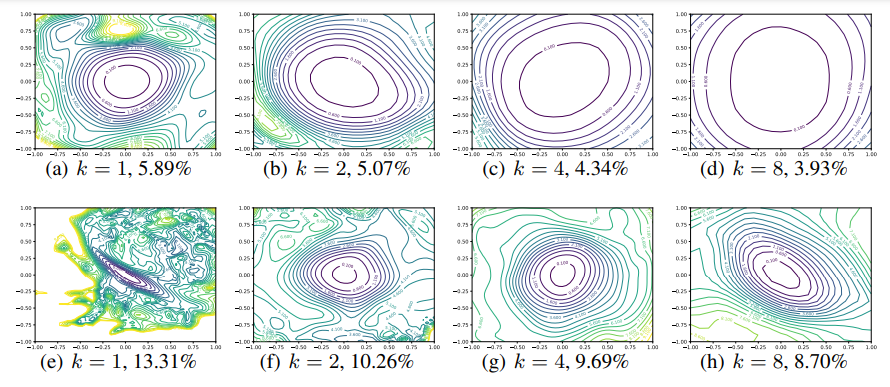
 wide해질 수록(=k가 커질 수록) chaotic한 곳들이 사라지고 볼록한 영역이 넓어지고 평면이 flat해짐을 볼 수 있다. 또한 self-connection이 minimizer를 많이 넓힘을 볼 수 있었다. 마지막으로 sharpness는 error와 비례한다.

 

Visualizing Optimization Paths

마지막으로 최적화 함수의 경로를 시각화한다.

random direction을 사용한 'Filter-Wise Normalization'로는 최적화 함수의 경로를 추적하기 힘들다 한다. 

Figure6. Ineffective visualizations of optimizer trajectories

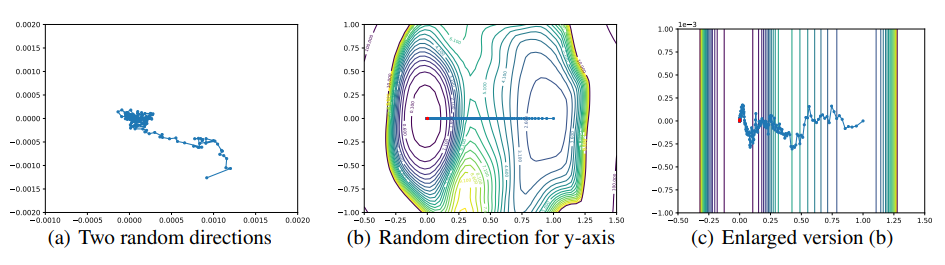
(a)를 통해 Two random directions을 이용한 시각화로는 최적화함수의 경로를 거의 포착하지 못함을 볼 수 있다. (b)는 한 축은 초기값의 값을 사용하고 한축은 random direction을 사용했는데, 이 방법도 궤적을 올바르게 나타내지 못해 경로를 직선으로 나타낸다(y축의 변화량을 잡아내지 못한다). 마지막으로 축을 random하게 선택했을 때는 손실함수가 직선임을 볼 수 있다.

이는 고차원의 랜덤백터 둘은 서로 orthogonal하기 때문이다. 따라서 저차원으로 시각하였을때도 orthogonal하여 변화량을 거의 표현할 수 없다. 이를 해결하기 위해 PCA라는 방법으로 궤적을 시각화한다.

 

PCA는 i번째 에폭에서 파라미터 θi, 학습이 끝난 후의 파라미터 θn로 행렬 M= [θ0−θn; · · · ; θn−1−θn]를 만들고 주성분 두개로 궤적을 시각화하는 방법이다.

 

Figure7. Projected learning trajectories use normalized PCA directions, left one uses batch size 128 and the right one uses batch size 8192

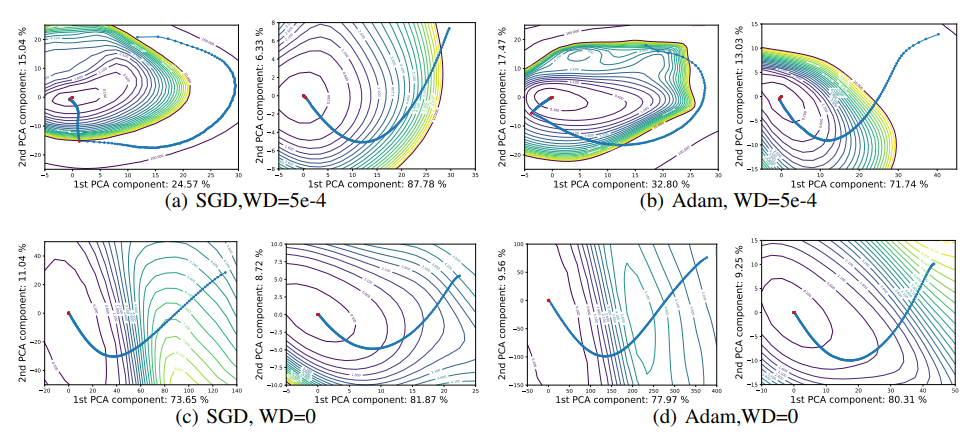
PCA를 이용해 최적화 함수의 경로를 나타낸 그림이다. 변화를 잘 포착하는 걸 볼 수 있다. Weight Decay를 사용하고 배치의 크기가 작을때는 등치선에 평행하게 궤도를 그린다. 빨간점은 학습률이 감소된 지점들인데 모든 최적화 경로들의 궤도가 local minimum으로 떨어지는 것을 볼 수 있다.

 

Conclusion

 모델의 구조, 배치 사이즈의 영향, 최적화함수 그리고 weight decay와 skip-connection 등이 손실함수의 모양과 최적화 함수의 경로에 어떤 영향을 끼치는지를 시각적으로 볼 수 있는 논문이였다. 모델을 설계할 때 선험적으로 판단하는 경우가 많은데 시각적으로 손실함수를 표현함으로써 그 기술들이 좋은 이유에 대한 근거가 늘어난 것 같다. 다만 논문을 처음 읽어봐 논문을 따라가는데만 집중하고 논문의 내용을 반박하거나 완전히 내것으로 하는데는 무리가 있는것 같다.